TEOREMAS DE LÍMITES CLASE 1

              21/01/23                 

 TEOREMAS DE LÍMITES

 El 21 de enero en clases  vimos que una función es aquella que tiene un valor de X para un valor de Y asi como tambien aprendí que existen 9 teoremas de límites y que no es necesario aprendernos todos.  

 El concepto de límite es la base fundamental con la que se construye el cálculo infinitesimal (diferencial e integral). Informalmente hablando se dice que el límite es el valor al que tiende una función cuando la variable independiente tiende a un número determinado o al infinito.

Para facilitar la obtención del límite de una función sin tener que recurrir cada vez a la definición Épsilon-Delta se establecen los siguientes teoremas.

Los teoremas se numeran consecutivamente para facilitar una futura referencia.

 Teorema de límite 1:

Si  k es una constante y a un número cualquiera, entonces

 Teorema de límite 2:

Para cualquier número dado a,

 Teorema de límite 3:

Si m y b son dos constantes cualesquiera, entonces

 Teorema de límite 4:

 Teorema de límite 5:

 Teorema de límite 6:

Si  f es un polinomio y a es un número real, entonces

 Teorema de límite 7:

Si q es una función racional y a pertenece al dominio de q, entonces

 Teorema de límite 8:

 

Procedimiento para calcular límites      Si es posible aplicar directamente las propiedades anteriores, el límite se calcula directamente. Con respecto a las propiedades, como la propiedad 6 se aplica a cualquier polinomio y las propiedades 1, 2, 3, y 4  implican funciones polinómicas es indistinto que nos refiramos a cada una de las propiedades 1 a 4 en particular que a la propiedad 6 cuando calculamos el límite de una función polinómica. Lo mismo, la propiedad 7 se aplica a una función racional y la propiedad 4 (III) también.      Cuando al sustituir la a por x en la función nos da la forma indeterminada 0/0 es posible calcular el límite pero, previamente, hay que transformar la fórmula de la función de tal modo que, una vez hecha la simplificación pertinente, se pueda evitar la división por cero: para lograr esto disponemos de procedimientos algebraicos eficaces como la factorización, la conjugada, etc.

Ejercicios resueltos           Evalué los siguientes límites indicando la propiedad o propiedades que se aplican en cada paso:

SOLUCIONES

 1. Solución

 2. Solución:

 3. Solución:

 4. Solución:

 5. Solución:

 6. Solución:

No es posible aplicar directamente el TL7, pues se obtendría la forma indeterminada 0/0; no obstante, luego de factorizar y simplificar la expresión, se obtiene fácilmente el límite aplicando el TL1:

 7. Solución:

No es posible aplicar directamente el TL7, pues se obtendría la forma indeterminada 0/0; no obstante, luego de factorizar y simplificar la expresión se obtiene fácilmente el límite aplicando el TL7 o el TL4(III):

 8. Solución:

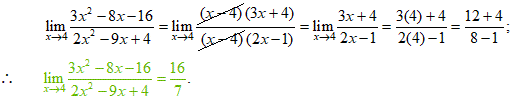
Si pretendiéramos aplicar el límite directamente a partir del TL7, nos daría la forma indeterminada 0/0;

por lo que, se debe factoriazar y luego simplificar la expresión antes de poder hacer uso del TL6:

 9. Solución:

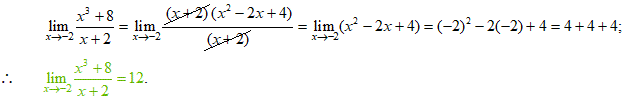
No se puede aplicar el límite directamente, daría la forma indeterminada 0/0; no obstante, luego de multiplicar tanto el numerador como el denominador por la conjugada de la expresión en el numerador y luego reduciendo y simplificando, se puede aplicar el TL para hallar el límite:

 10. Solución:

Luego de la transformación de la expresión se aplican los TL7  y  TL8:

 11. Solución:

El límite no se puede aplicar directamente, resultaría la forma indeterminada 0/0; no obstante, una vez factorizando y simplificando, la expresión queda expedita para hallar el límite mediante los TL7  y  TL6:

 12. Solución:

REFERENCIAS QUE AGREGUE DE DONDE ESTUVE VIENDO MAS INFORMACIÓN SOBRE LOS TEOREMAS DE LIMITES: 

https://www.calculo.jcbmat.com/id301.htm

https://youtu.be/6n-JDv3ddM4